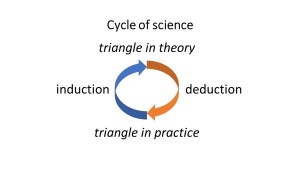
There is a well-known alternation of induction and deduction in science (click to enlarge):
The induction phase consists of data collection, data analysis, and model development. The deduction phase consists of taking the model, making hypothetical inferences, and following up with experiments that lead to new data collection. Then the cycle repeats.
One side of the cycle is focused on practice and the other side on theory. Induction results in definitions, postulates, and new theory. Deduction results in inferences, experiments, and new practice.
One question is whether this cycle should begin with the practice side or the theory side:
The realist begins with practice and the induction phase. The anti-realist begins with theory and the deductive phase. An anti-realist will invent a hypothesis in order to begin. A realist will discover some interesting observations in order to begin.
Mathematics works exclusively with deduction. Probability is an example of mathematics. What is the subject that works exclusively with induction? I’m calling it simply generalizations. Statistics is an example of a discipline that generalizes.
As a simple example, consider the triangle:
In ancient times no doubt triangular shapes were observed, and then someone abstracted the concept triangle. Euclid came along and placed triangles in his geometric theory. Theorems were deduced and applied in practice. The development of mathematics shows how science works.